Lagrangian Points - Gateway to the Solar System

What is next after a Earth orbiting space station and a moon base?  

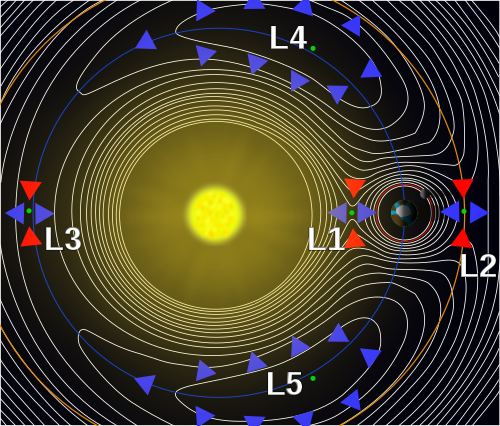
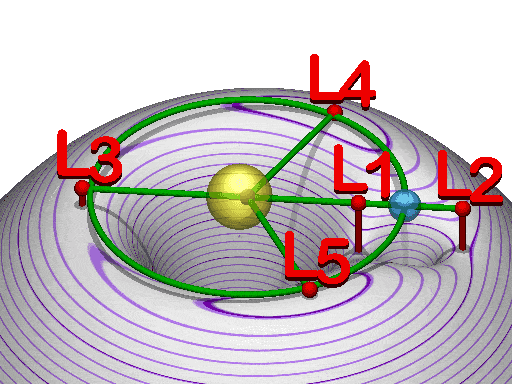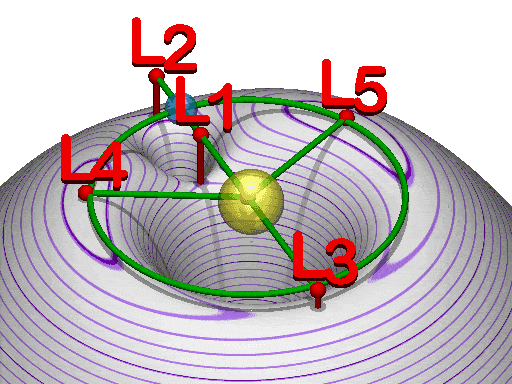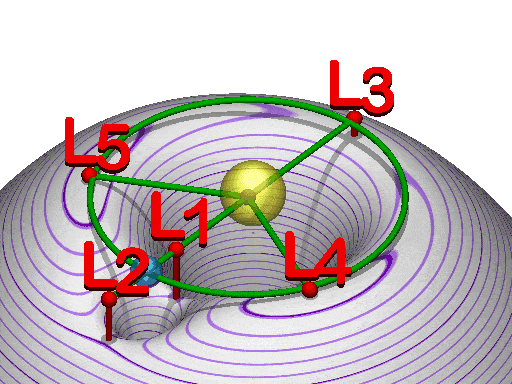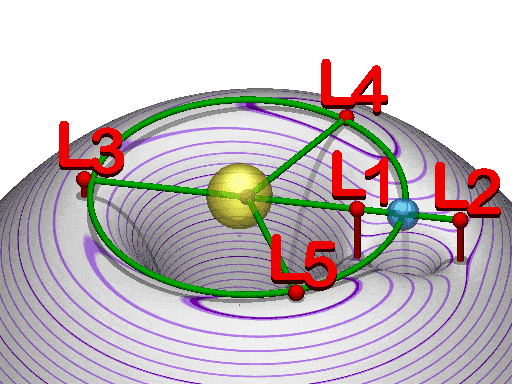
There are five "stable" points in space around the Earth and Sun where the forces of gravity and centripetal force from orbits cancel out.  These are called Lagrangian points (L1-L5) and they are all well outside the moons orbit.  L1 is the easiest to think about.  It is the point between the sun and earth where the attraction of the two bodies from gravity (and factoring in outward orbital forces) cancel out.  (At this point a small nudge toward the sun will result in movement closer to the sun; a small nudge toward earth will result in movement toward earth.)  L2 and L3 are in (relative) stationary orbit around the combined Earth-Sun system (small nudges can move them increasingly toward or increasingly away from the combined system). 

Original found here. 

L4 and L5 are less intuitive.  They are also in orbit around the combined system; in fact, they are the points of an equilateral triangle with the Earth and Sun at two of the points.  They seem to be constantly falling toward or away from Earth in its orbit.  L4 and L5 also tend to collect asteroids and might be a target for space mining near Earth.

Original found here. 

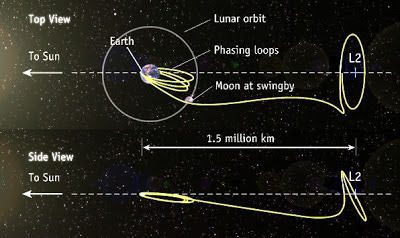
L2 is of particular interest since it is partially shielded from solar radiation by the Earth.  It is 1,500,000 km away, almost four times the distance to the moon, and sits just outside full protection by the magnetic field. 

The interesting thing about these points is that getting from one to another takes very little energy.  A slight push in the right direction can put a payload with a large mass into a trajectory to end up at the next point.  This makes the L-points ideal for space stations to route supplies and missions.  Contrast this to the enormous cost of getting a pound of material up off the Earths surface to even low earth orbit.

In addition to moving toward or away from the system, in a complex way objects can "orbit" the Lagrangian points.  Their orbits are actually controlled by the interplay of Earth and Sun gravities, but the end result is that they appear to orbit a point of empty space.  The L-point orbits are complex because more than two objects are interacting and in motion at the same time.  There are "halo" and "lissajous" orbits that are not "flat" in a plane like orbits we are used to thinking about but move in three dimensions.   A neat example uses the moon to boost an object from Earth orbit out to orbit "around" L2. 

In fact, this idea can be extended to include Lagrangian points of other planets in the solar system.  If you can get to the Earth-Sun L2 you can get to any other plants Lagrangian points with very little energy, just with some nudges in the right direction.  (With more energy you can get there faster by taking shortcuts through places with gravity/orbital forces to overcome.)  A highly stylized conception from NASA of an interplanetary network is below.

Original found here.

It makes a lot of sense for NASA to be thinking about using these L-points for the next phases of manned missions and building up space based infrastructure to make future missions possible.